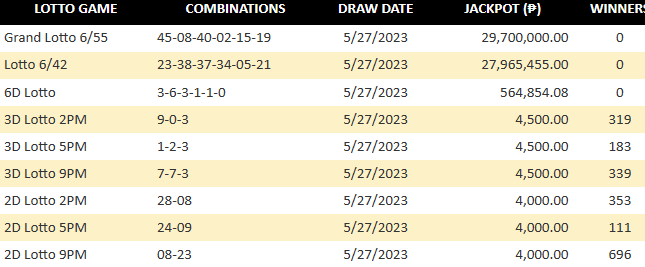
The Grand Lotto 6/55 is a lottery game where players choose six numbers from a pool of 55 numbers. To calculate the number of combinations in this game, we can use the formula for calculating combinations, which is given by:
C(n, r) = n! / (r!(n-r)!)
where n is the total number of items to choose from (55 in this case), and r is the number of items to choose (6 in this case).
Using this formula, we can calculate the number of combinations for the Grand Lotto 6/55 as follows:
C(55, 6) = 55! / (6!(55-6)!) = 55! / (6!49!)
Here, the exclamation mark (!) denotes the factorial function, which means multiplying a number by all the positive integers less than it down to 1.
Calculating the factorial of 55:
55! = 55 × 54 × 53 × … × 3 × 2 × 1
Similarly, calculating the factorial of 6 and 49:
6! = 6 × 5 × 4 × 3 × 2 × 1 49! = 49 × 48 × 47 × … × 3 × 2 × 1
Substituting these values into the formula:
C(55, 6) = 55! / (6!49!) = (55 × 54 × 53 × … × 3 × 2 × 1) / ((6 × 5 × 4 × 3 × 2 × 1) × (49 × 48 × 47 × … × 3 × 2 × 1))
Calculating this expression gives us the total number of combinations in the Grand Lotto 6/55.
How many combinations are there in Grand Lotto 6/55? - Article Content Statement
You are now seeing the article How many combinations are there in Grand Lotto 6/55?, or the PCSO Lotto results in website, are collected from the internet, if there is an error in the results of PCSO lottery results on this site, please refer to the official PCSO lottery results.